[TOC]

1. Two Sum(两数之和)

思路

嵌套两次循环 O(n*n)
两个一次循环 O(2n)
一次循环

两个一次循环 O(2n)

第一次循环用 hashmap 存储所给的数据
第二次循环用 target - 当循环当前的值得到sub，判断 sub 是否在 map 中，同时 sub 不能是当前的值

public static int[] twoSum(int[] nums, int target) {
      Map<Integer, Integer> cache = new HashMap<>();
      for (int i = 0; i < nums.length; i++) {
          cache.put(nums[i], i);
      }
      for (int i = 0; i < nums.length; i++) {
          int sub = target - nums[i];
          if (cache.containsKey(sub) && cache.get(sub) != i) {
              return new int[]{i, cache.get(sub)};
          }
      }
      return null;
  }

一次循环

将两次循环合并，不用判断当前的值和 sub 是否一样，只将遍历到的值存入 map 中。

Map<Integer, Integer> cache = new HashMap<>();
   for (int i = 0; i < nums.length; i++) {
       int sub = target - nums[i];
       if (cache.containsKey(sub)) {
           return new int[]{i, cache.get(sub)};
       }
       cache.put(nums[i] , i);
   }
   return null;

2. Add Two Numbers (两数相加)

思路

一开始想的是遍历两个链表，把他们变成十进制数，然后相加，最后再把这个数转化成链表，但是题目给的条件是 [1，100] 位数的范围，传统的 64 位用java 是表示不出来的。

同时遍历两个链表，在相同长度内相加，进位传递下一次遍历
如果有一个链表遍历结束，以后它所有的 val 值都是 0

code

public class PRC_02 {

    public static class ListNode {
        int val;
        ListNode next;

        ListNode() {
        }

        ListNode(int val) {
            this.val = val;
        }

        ListNode(int val, ListNode next) {
            this.val = val;
            this.next = next;
        }
        
    }

    public static ListNode addTwoNumbers(ListNode l1, ListNode l2) {

        int digit = 0;
        ListNode head = new ListNode(0);
        ListNode cur = head;

        while (l1 != null || l2 != null) {
            int x = l1 != null ? l1.val : 0;
            int y = l2 != null ? l2.val : 0;

            int val = digit > 0 ? (x + y + digit) : (x + y);

            digit = val / 10;

            cur.next = new ListNode(val % 10);
            cur = cur.next;

            if (l1 != null) l1 = l1.next;
            if (l2 != null) l2 = l2.next;
        }
        if (digit != 0) {
            cur.next = new ListNode(digit);
        }

        return head.next;
    }

    public static void main(String[] args) {


        // case 1
        ListNode n1 = new ListNode(4, null);
        ListNode n2 = new ListNode(6, n1);
        ListNode n3 = new ListNode(5, n2);

        ListNode n4 = new ListNode(3, null);
        ListNode n5 = new ListNode(4, n4);
        ListNode n6 = new ListNode(2, n5);

        ListNode listNode = addTwoNumbers(n3, n6);


        //case 2
     /*   ListNode n1 = new ListNode(9,null);


        ListNode n2 = new ListNode(9, null);
        ListNode n3 = new ListNode(9, n2);
        ListNode n4 = new ListNode(9, n3);
        ListNode n5 = new ListNode(9, n4);
        ListNode n6 = new ListNode(9, n5);
        ListNode n7 = new ListNode(9, n6);
        ListNode n8 = new ListNode(9, n7);
        ListNode n9 = new ListNode(9, n8);
        ListNode n10 = new ListNode(9, n9);
        ListNode n11 = new ListNode(1, n10);


        System.out.println(calListNode(n1) );
        System.out.println(calListNode(n11));

        ListNode listNode = addTwoNumbers(n1, n11);*/
        System.out.println(1);

    }
}

3. Longest Substring Without Repeating Characters (无重复字符的最长子串)

思路

一开始看到无重复是想用 Set，然后用两层循环，最后打出 Set 的长度，但是吧，我不喜欢用两次循环，所以考虑到了双指针。

用双指针（滑动窗口）确定字符串的连续
用 Set 确保不重复
用一个变量确定最长的长度

AC ( 待优化)

public class PRC_03 {
    public static int lengthOfLongestSubstring(String s) {
        char[] chars = s.toCharArray();
        int length = chars.length;
        int left = 0 ;
        int right = 0;
        int maxlength = 0;

        Set<Character> set = new HashSet<>();

        while (left <= right  && right < length) {
            if (set.add(chars[right])) {
                maxlength = Math.max(maxlength, right - left + 1);
                right++;
                continue;
            }
            set.clear();
            left++;
            right = left;
        }

        return maxlength;
    }


    public static void main(String[] args) {

        System.out.println(lengthOfLongestSubstring("abcabcbb"));
        System.out.println(lengthOfLongestSubstring("bbbbb"));
        System.out.println(lengthOfLongestSubstring("pwwkew"));
        System.out.println(lengthOfLongestSubstring("au"));
        System.out.println(lengthOfLongestSubstring("aab"));
        System.out.println(lengthOfLongestSubstring("dvdf"));


    }
}

4. Median of Two Sorted Arrays (寻找两个正序数组的中位数)

思路

有序归并

AC

public class PRC_04 {

    public static double findMedianSortedArrays(int[] nums1, int[] nums2) {

        int[] merge = merge(nums1, nums2);

        int length = merge.length;

        return length % 2 == 0 ? (double) (merge[length / 2 - 1] + merge[length / 2]) / 2 : merge[length / 2];
    }

    public static int[] merge(int[] nums1, int[] nums2) {
        int[] merged = new int[nums1.length + nums2.length];
        int left = 0;
        int right = 0;
        int index = 0;

        while (left < nums1.length || right < nums2.length) {

            if (left >= nums1.length) {
                merged[index++] = nums2[right];
                right++;
            } else if (right >= nums2.length) {
                merged[index++] = nums1[left];
                left++;
            } else if (nums1[left] < nums2[right]) {
                merged[index++] = nums1[left];
                left++;
            } else {
                merged[index++] = nums2[right];
                right++;
            }
        }
        return merged;
    }

    public static void main(String[] args) {
        //case1
        int[] nums1 = new int[]{1, 3};
        int[] nums2 = new int[]{2};

        //case2
//        int[] nums1 = new int[]{1, 2};
//        int[] nums2 = new int[]{3,4};


//        int[] merge = merge(nums1, nums2);
        double medianSortedArrays = findMedianSortedArrays(nums1, nums2);

//        System.out.println("merged array: " + Arrays.toString(merge));
        System.out.println(medianSortedArrays);


    }
}

5. Longest Palindromic Substring (最长回文子串)

思路

对称结构，我想中间往外拓展的查找，但是发现逻辑比较繁琐
双重循环，很笨重的方法
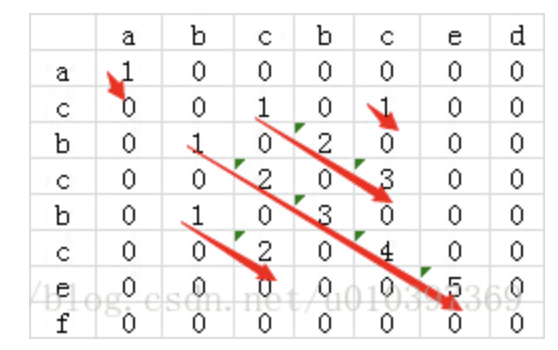
最终没有写出来，参考的别人动态规划的思路，既然是回文数，那它字符串自身反转也是拥有着这个回文数的，用一个对称的二维数据，去计算结果

AC(动态规划，求最长公共字串，最后找回文)

public class PRC_05 {

    public static String longestPalindrome(String s) {
        if(s.equals("")){
            return "";
        }
        StringBuilder reverse = new StringBuilder(s).reverse();
        int n = s.length();
        int[][] arr = new int[n + 1][n + 1];
        int left = 0;
        int right = 0;
        int max = 0;
        for (int i = 1; i <=n; i++) {
            for (int j = 1; j <= n; j++) {
                if (s.charAt(i - 1) == reverse.charAt(j - 1) ) {
                    arr[i][j] = arr[i - 1][j - 1] + 1;
                }else{
                    arr[i][j] = 0;
                }

                if( arr[i][j] > max ){
                    int beforeRev = n - j - 1 - 1;
                    if (beforeRev + arr[i][j] + 1 + 1 == i  ) {
                        max = arr[i][j];
                        left = i - max ;
                        right = i ;
                    }
                }
            }
        }

        return s.substring(left , right );

    }

    public static void main(String[] args) {

        //case 1
//        String s = "babad"; i 3 j =3 n = 5 max = 3

//        0 2
        //case 2
//        String s = "cbbd";

        //case 3
//        String s = "ac";

        //case 4
//        String s = "ccc";
//        String s = "abb";
//        String s = "a";
        String s = "aacabdkacaa";


        System.out.println(longestPalindrome(s));

    }

//                   [[0, 0, 0, 0, 0, 0],
//                    [0, 1, 0, 1, 0, 0],
//                    [0, 0, 2, 0, 2, 0],
//                    [0, 1, 0, 3, 0, 0],
//                    [0, 0, 0, 0, 0, 0],
//                    [0, 0, 0, 0, 0, 0]]

}

AC 中心扩展

class Solution {
    public String longestPalindrome(String s) {
     
     int maxLength = 0;
        String res = "";

        for (int i = 0; i < s.length(); i++) {
            String s1 = centerExpand(s, i, i);
            String s2 = centerExpand(s, i, i + 1);
            String max = s1.length() > s2.length() ? s1 : s2;
            if (max.length() > maxLength) {
                maxLength = max.length();
                res = max;
            }
        }
        return res;
    }

     public  String centerExpand(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            left --;
            right ++;
        }
        return s.substring(left + 1, right);
    }
}

6. 3Sum (三数之和)

回溯，超时间复杂度，就是 Cn3，然后去重嘛
双指针

AC(自己两年的代码，现在的我竟然看不懂，而且写不出来)

public class PRC_15 {
    public static List<List<Integer>> threeSum(int[] nums) {
        int n = nums.length;
        Arrays.sort(nums);
        List<List<Integer>> ret = new ArrayList<>();

        for( int first = 0; first < n ; first++){

            if( first > 0 && nums[first]==nums[first-1]){
                continue;
            }
            int third = n -1;
            int target = -nums[first];

            for( int second = first + 1 ; second < n ; second++){
                if(second > first + 1 && nums[second]==nums[second-1]){
                    continue;
                }

                while( second < third && nums[second ]+ nums[third ] > target){
                    third--;
                }

                if(third==second){
                    break;
                }

                if(nums[third] + nums[second]== target){
                    ret.add(List.of(nums[first], nums[second], nums[third]));
                }
            }
        }

        return ret;
    }

    public static void main(String[] args) {
        // [-1,0,1,2,-1,-4]
//        -4, -1,-1, 0 , 1, 2
//        int[] array = new int[]{-1, 0, 1, 2, -1, -4};
        int[] array = new int[]{1,1,-2};

        List<List<Integer>> lists = threeSum(array);
        System.out.println(1);

    }
}

7. Maximum Subarray (最大子序和)

思路

参考最长子序列，用一个二维数组存储，但是空间超标
换一个 dp 的思路， dp[i] 当前是前 i 个最大的子串和，如果 dp[i - 1] < 0 说明，i - 1 之前最大都是负数，那么就舍去它，换上当前元素的值，只要用 max 和 dp[i] (也就是 nums[i]) 做比较，就能算出最大值
如果 dp[i - 1] > 0 那就加上 nume[i] , 算出第 i 长的子序最大值。

AC

public class PRC_53 {

    public static int maxSubArray(int[] nums) {

        int n = nums.length;
        int max = nums[0];
        int[] dp = new int[n];


        dp[0] = nums[0];

        for(int i = 1 ; i <n ; i++) {
            if (dp[i - 1] < 0) {
                dp[i] = nums[i];
            }else{
                dp[i] = dp[i - 1] + nums[i];
            }
            max = Math.max(dp[i], max);
        }

        return max;
    }



    public static void main(String[] args) {
        int[] nums = new int[]{-2, 1, -3, 4, -1, 2, 1, -5, 4};
        System.out.println(maxSubArray(nums));

    }
}

8. Reverse Integer (整数反转)

思路

不动脑子思路，直接 api 往死里dui
取余取整数，循环位移，记得判断溢出

AC（不动脑子做法）

public class PRC_07 {
    public static int reverse(int x) {
        boolean negative = x < 0;
        String s = String.valueOf(x);
        StringBuilder builder = new StringBuilder();
        int zeroIndex = Integer.MIN_VALUE;
        for (int i = s.length() - 1 ; i >= 0 ; i--) {
            if(s.charAt(i) != 0){
                zeroIndex = i;
                break;
            }
        }
        for(int i = zeroIndex ; i >= 0 ; i--) {
            if(s.charAt(i) == '-'){
                continue;
            }
            builder.append(s.charAt(i));
        }
        String s1 = negative ? "-"+builder.toString() : builder.toString();
        int i = 0;
        try {
            i = Integer.parseInt(s1);
        } catch (NumberFormatException e) {
            return 0;
        }

        return i;
    }

    public static void main(String[] args) {
        System.out.println(reverse(1534236469));
    }
}

9.Container With Most Water (盛最多水的容器)

思路

空间排除法
双指针思路，短板确定最大的容器大小，所以短板之后所有的只会小于等于当前的容器大小
我们要确定左右那个到底是短板，然后根据短板的位置进行对应的移动
右边的短板，那就左移动，左边是短板，那就右移动，直到双指针相遇
短板的移动，可以获得未来的不确定性，将当前的 maxSize 和不确定性的大小做比较
优秀题解

AC

历史提交记录

public class PRC_11 {
    public static int maxArea(int[] height) {

        int left = 0;
        int right = height.length - 1;
        int maxSize = Integer.MIN_VALUE;

        while (left < right) {

            // 确定短板，右移或者左移，
//            if (height[left] < height[right]) {
//                // 左边为短板,最大size 就是 right-left * height[left]
//                maxSize = Math.max(maxSize, (right - left) * height[left]);
//                left++;
//
//            } else if (height[left] > height[right]) {
//                // 右边为短板 , max = right  - left * height[right]
//                maxSize = Math.max(maxSize, (right - left) * height[right]);
//                right--;
//            }

            maxSize = height[left] < height[right] ?
                    Math.max(maxSize, (right - left) * height[left++]) :
                    Math.max(maxSize, (right - left) * height[right--]);
        }

        return maxSize;
    }
    public static void main(String[] args) {
        int[] height = new int[]{1,8,6,2,5,4,8,3,7};
        System.out.println(maxArea(height));
    }
}

10.Trapping Rain Water (接雨水)

思路

DP, 找到当前列左边最大，和右边最大，取两者最小的
然后和当前的height 比较，如果大于当前 height 就 sum +，否则 continue

AC

public class PRC_42 {
    public static int trap(int[] height) {

        // 记录 i 之前 左边座高的墙
        // 记录 i 之前 右边最高的墙
        int[] max_left = new int[height.length];
        int[] max_right = new int[height.length];
        int sum = 0;

        for (int i = 1; i < height.length - 1; i++) {
            max_left[i] = Math.max(height[i - 1], max_left[i - 1]);
        }
        for (int i = height.length - 2; i >= 0; i--) {
            max_right[i] = Math.max(height[i + 1], max_right[i + 1]);
        }

        for (int i = 1; i < height.length - 1; i++) {
            int min = Math.min(max_right[i], max_left[i]);
            if (min > height[i]) {
                sum += min - height[i];
            }

        }

        return sum;
    }

    public static void main(String[] args) {
        int[] height = new int[]{0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};
        System.out.println(trap(height));
    }

}

11. Valid Parentheses (有效的括号)

思路

用栈

AC

public class PRC_20 {


    public static boolean isValid(String s) {

        Stack<Character> stack = new Stack<>();
        stack.push(s.charAt(0));
        for (int i = 1; i < s.length(); i++) {
           if (!stack.isEmpty() && (s.charAt(i) - stack.peek() == 1 || s.charAt(i) - stack.peek() == 2)) {
                stack.pop();
            }else{
                stack.push(s.charAt(i));
            }
        }
        return stack.isEmpty();

    }

    public static void main(String[] args) {

        String s = "({[)";
        System.out.println(isValid(s));

    }
}

树专题

12. 二叉树的最大深度

思路

解法一，记录当前遍历的层数，取最大值
解法二，分解为左右子树的子问题，子树最大的 depth + 1
层序遍历

AC（M1）

public class PRC_104 {

    int maxDepth;
    int curDepth;

    public int maxDepth(TreeNode root) {

        traverse(root);
        return maxDepth;
    }

    public void traverse(TreeNode node) {
        if (node == null) {
            return;
        }

      // 前序位置
      	curDepth++;
        if (node.left == null && node.right == null) {
            maxDepth = Math.max(maxDepth, curDepth);
        }
        traverse(node.left);
      // 中序 位置
        traverse(node.right);

      // 后序位置
        curDepth--;

    }

    public static void main(String[] args) {
        PRC_104 prc104 = new PRC_104();

        TreeNode treeNode3 = new TreeNode(3);
        TreeNode treeNode9 = new TreeNode(9);
        TreeNode treeNode20 = new TreeNode(20);
        TreeNode treeNode15 = new TreeNode(15);
        TreeNode treeNode7 = new TreeNode(7);

        treeNode3.left  = treeNode9;
        treeNode9.left = null;
        treeNode9.right = null;
        treeNode15.right = null;
        treeNode15.left = null;
        treeNode7.right = null;
        treeNode7.left = null;
        treeNode3.right = treeNode20;
        treeNode20.left = treeNode15;
        treeNode20.right = treeNode7;


        int i = prc104.maxDepth(treeNode3);
        System.out.println("Max depth : " + i);
    }
}

AC(M2)

public int maxDepth2(TreeNode root) {
      if (root == null) {
          return 0;
      }
      int maxLeft = maxDepth(root.left);
      int maxRight = maxDepth(root.right);

      return Math.max(maxLeft, maxRight) + 1;
  }

13. 二叉树的前序遍历

思路

就是 traverse 完事

AC(M1)

public class PRC_144 {
    public List<Integer> preorderTraversal(TreeNode root) {

        List<Integer> res = new ArrayList<>();
        traverse(root, res);
        return res;

    }

    public void traverse(TreeNode node, List<Integer> preOrderList) {
        if (node == null) {
            return;
        }

        preOrderList.add(node.val);
        traverse(node.left, preOrderList);
        traverse(node.right, preOrderList);

    }

}

AC(M2)

public List<Integer> preorderTraversal(TreeNode root) {

       List<Integer> res = new ArrayList<>();
       if (root == null) {
           return res;
       }
       res.add(root.val);
       res.addAll(preorderTraversal(root.left));
       res.addAll(preorderTraversal(root.right));
       
       return res;

   }

AC(M3)

public int maxDepth3(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int count = 0;
        while(!queue.isEmpty()){
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode curNode = queue.poll();
                if (curNode.left != null) {
                    queue.offer(curNode.left);
                }
                if (curNode.right != null) {
                    queue.offer(curNode.right);
                }
            }
            count++ ;
        }
        return count;
    }

14. 二叉树的直径

思路

左右子树最大 depth 之和

AC

public class PRC_543 {

    int maxDiameter ;
    public int diameterOfBinaryTree(TreeNode root) {
        maxDepth(root);
        return maxDiameter;

    }


    public int maxDepth(TreeNode root ){
        if(root == null) return 0;
        int maxLeft = maxDepth(root.left);
        int maxRight = maxDepth(root.right);
        int curDiameter = maxLeft + maxRight;
        maxDiameter = Math.max(curDiameter, maxDiameter);

        return Math.max(maxLeft, maxRight) + 1;
    }
}

15.翻转二叉树

思路

遍历
子问题合并

AC（M1）

public class PRC_226 {
    public TreeNode invertTree(TreeNode root) {
        traverse(root);
        return root;
    }


    public void traverse(TreeNode node) {
        if (node == null) {
            return;
        }
        TreeNode tempNode = node.left;
        node.left = node.right;
        node.right = tempNode;
        traverse(node.left);
        traverse(node.right);
    }
}

AC(M2)

public TreeNode invertTree1(TreeNode root) {
       if(root == null) return null;
       TreeNode leftRoot = invertTree1(root.left);
       TreeNode rightRoot = invertTree1(root.right);

       root.left = rightRoot;
       root.right = leftRoot;
       return root;
   }

16.填充每个节点的下一个右侧节点指针

思路

一开始想到的是层序遍历但是比较麻烦
想不到其他办法，看的题解，转化成三叉树，主要是，不同父节点的左右结点的连接。

AC

public class PRC_116 {

    public Node connect(Node root) {
        if (root == null) {
            return null;
        }
        traverse(root.left, root.right);
        return  root;
    }


    public void traverse(Node node1, Node node2) {
        if (node1 == null || node2 == null) {
            return;
        }

        node1.next = node2;

        traverse(node1.left, node1.right);
        traverse(node2.left, node2.right);
        traverse(node1.right, node2.left);
    }
}

17. 二叉树展开为链表

思路

分解为左右子树的子问题。
将 root 的 right 全部左子树（已经是链表了），在左子树的最后 append 上右子树。

AC

public void flatten(TreeNode root) {
        if (root == null) {
            return ;
        }
        flatten(root.left);
        flatten(root.right);

        TreeNode left = root.left;
        TreeNode right = root.right;
        root.left = null;
        root.right = left;


        TreeNode dummyHead = root;
        while (dummyHead.right != null) {
            dummyHead = dummyHead.right;
        }

        dummyHead.right = right;
    }

18.最大二叉树

思路

利用快速排序中的 partion 分区的思想，处理子问题
最后合并成完整的一棵树
递归的时候，要有局部变量的思维

AC

 public TreeNode constructMaximumBinaryTree(int[] nums) {
        return build(nums, 0, nums.length - 1);
    }

    public TreeNode build(int[] nums, int begin, int end) {
        if(begin > end) return  null;

        int maxIndex = -1;
        int maxVlaue = Integer.MIN_VALUE;
        for (int i = begin; i <= end; i++) {
            if (nums[i] > maxVlaue) {
                maxIndex = i;
                maxVlaue = nums[i];
            }
        }
        // 错误写法，maxIndex = 0 不管是左右 都会和 这个做比较 ，应该是只和 maxValue 做比较
   //   可以把 maxIndex = begin; 这样子就对了
//        int maxIndex = 0;
//        for (int i = begin; i <= end; i++) {
//            if (nums[i] > nums[maxIndex]) {
//                maxIndex = i;
//            }
//        }

        TreeNode root = new TreeNode(nums[maxIndex]);
        root.left  = build(nums, begin, maxIndex - 1);
        root.right = build(nums,maxIndex + 1, end);

        return root;

    }

19.从前序与中序遍历序列构造二叉树

思路

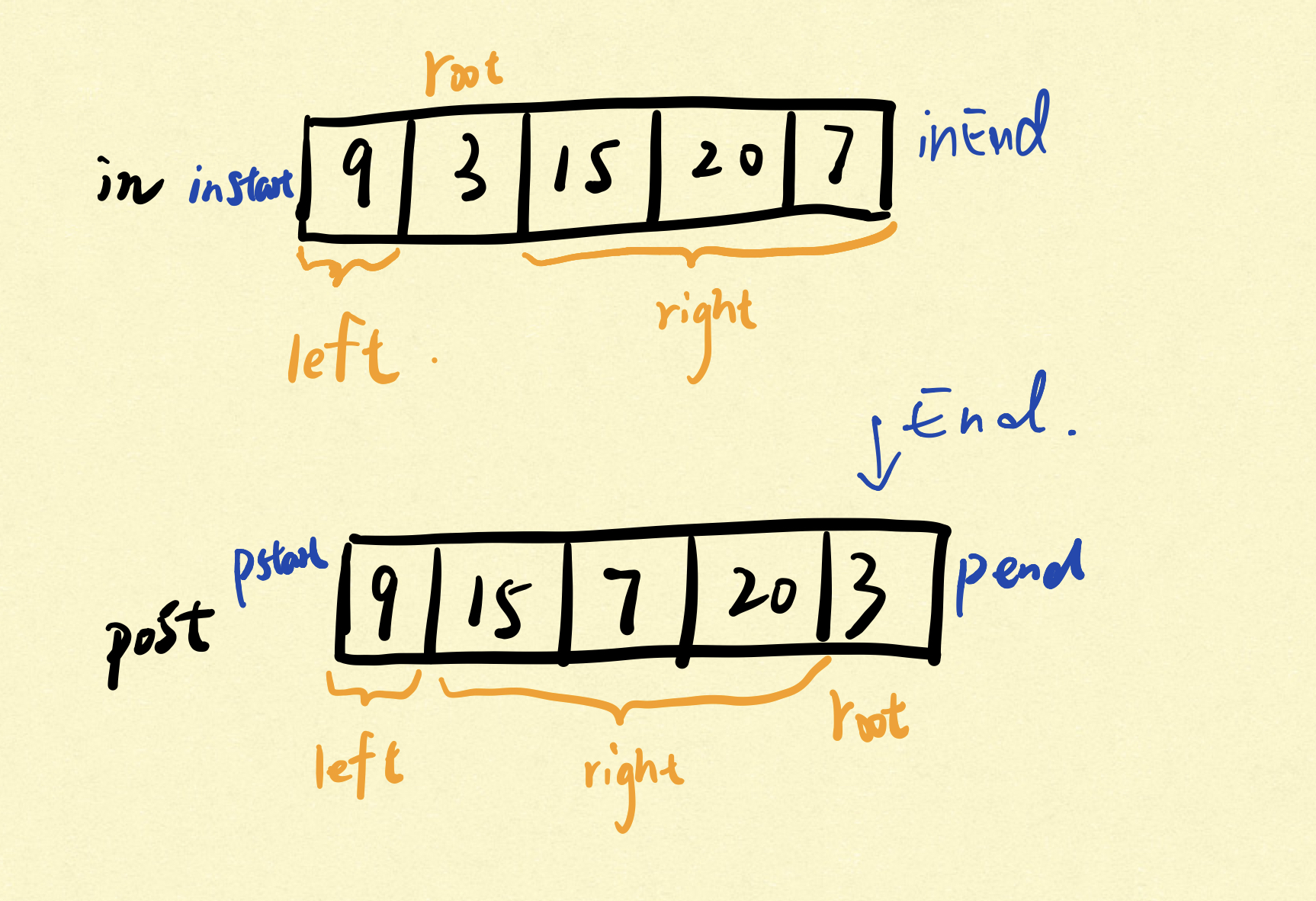
找到 preorder 和 inorder 的规律，根据规律进行递归
分解成子问题哈

AC

public class PRC_105 {

    Map<Integer, Integer> map  = new HashMap<Integer, Integer>();

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }

        return build(preorder, 0, preorder.length - 1
                , inorder, 0, inorder.length - 1);
    }

    public TreeNode build(int[] preorder, int preStart, int preEnd ,
                          int[] inorder , int inStart , int inEnd){

        if(preStart > preEnd){
            return null;
        }
        TreeNode root = new TreeNode(preorder[preStart]);
        Integer index = map.get(preorder[preStart]);
        int leftSize = index - inStart;

        root.left = build(preorder, preStart + 1, preStart + leftSize,
                inorder, inStart, index - 1);
        root.right = build(preorder, preStart + leftSize + 1, preEnd
                , inorder, index + 1, inEnd);

        return root;
    }
}

20. 从中序与后序遍历序列构造二叉树

思路

只能画图，找关系，和前一道题类似

思路草稿

AC（一遍过，思路及其正确）

public class PRC_106 {

    Map<Integer, Integer> map = new HashMap<Integer, Integer>();

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }

        return build(inorder, 0 , inorder.length - 1 , postorder , 0, postorder.length - 1);
    }


    public TreeNode build(int[] inorder, int inStart, int inEnd,
                          int[] postorder, int postStart, int postEnd) {

        if (postStart > postEnd) {
            return null;
        }

        int postRootVal = postorder[postEnd];

        Integer index = map.get(postRootVal);

        int rightSize = inEnd - index;

        TreeNode root = new TreeNode(postRootVal);

        root.left = build(inorder, inStart, index - 1, postorder, postStart, postEnd - rightSize  - 1);
        root.right = build(inorder, index + 1, inEnd, postorder, postEnd - rightSize, postEnd - 1);

        return root;


    }
}

21. 二叉树的序列化与反序列化

思路：

这里和之前的构造不同，不要被带进死胡同里去
随便用一种遍历方式，（用特定的规则）得到一个遍历数组 a ,
用定义的规则再去反序列化 a’ （删除了一些 null 的替代字符串）
最后再用中序去构造。

AC

package com.amberzxh.BinaryTree;

import java.awt.*;
import java.util.LinkedList;

/**
 * @Author: AmberZxh
 * @DateTime: 2023/2/19 17:11
 * @Description:
 */
public class PRC_297 {
    String SPLIT = ",";
    String NULL = "#";
    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        StringBuilder build = new StringBuilder();
        serialize(root, build);
        return build.toString();
    }
    public void serialize(TreeNode root, StringBuilder build) {
        if (root == null) {
            build.append(NULL).append(SPLIT);
            return;
        }
        build.append(root.val).append(SPLIT);
        serialize(root.left, build);
        serialize(root.right, build);
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        String[] split = data.split(SPLIT);
        LinkedList<String> inOrder = new LinkedList<>();
        for (String s : split) {
            inOrder.addLast(s);
        }
        return deserialize(inOrder);
    }
    public TreeNode deserialize(LinkedList<String> head) {
        String val = head.removeFirst();
        if (head.isEmpty() || val.equals(NULL)) {
            return null;
        }
        TreeNode root = new TreeNode(Integer.parseInt(val));
        root.left = deserialize(head);
        root.right = deserialize(head);
        return root;
    }
}

22.寻找重复的子树

思路：

第一肯定是遍历
关键是如何找到每一棵子树，用分解问题，最后归并，用个 string 存储当前子树字符串
用一个 HasMap 记录重复的子树，重复的只作为最后答案的一种

AC

package com.amberzxh.BinaryTree;

import java.util.*;
import java.util.concurrent.TransferQueue;

/**
 * @Author: AmberZxh
 * @DateTime: 2023/2/20 20:53
 * @Description:
 */
public class PRC_652 {
    Map<String, Integer> computer = new HashMap<String, Integer>();
    List<TreeNode> res = new ArrayList<>();

    public List<TreeNode> findDuplicateSubtrees(TreeNode root) {

        traverse(root);

        return res;

    }

    String SPLIT = ",";
    public String traverse(TreeNode root) {
        if (root == null) {
            return "#";
        }
        String left = traverse(root.left);
        String right  = traverse(root.right);
        String s = left + SPLIT + right + SPLIT + root.val;
        Integer appearCount = computer.getOrDefault(s, 0);
        if (appearCount == 1) {
            res.add(root);
        }

        computer.put(s, appearCount + 1);

        return  s;
    }

    public static void main(String[] args) {

        PRC_652 prc652 = new PRC_652();
        TreeNode treeNode = prc652.buildDemo();
        prc652.traverse(treeNode);
        System.out.println(prc652.computer);

    }


    public TreeNode buildDemo() {
        TreeNode root = new TreeNode(1);

        TreeNode treeNode1 = new TreeNode(2);
        TreeNode treeNode2 = new TreeNode(3);
        TreeNode treeNode3 = new TreeNode(4);
        TreeNode treeNode4 = new TreeNode(2);
        TreeNode treeNode5 = new TreeNode(4);
        TreeNode treeNode = new TreeNode(4);


        root.left = treeNode1;
        treeNode1.left = treeNode3;
        treeNode1.right = null;

        treeNode3.left = null;
        treeNode3.right = null;

        root.right = treeNode2;
        treeNode2.left = treeNode4;
        treeNode2.right =treeNode5;
        treeNode4.right= treeNode;
        treeNode.right = null;
        treeNode.left = null;
        treeNode5.right = null;
        treeNode5.left  = null;

        return root;
    }
}

23.归并排序（早就会了）

24.计算右侧小于当前元素的个数（hard）

思路:

用归并排序，当 swap left 和 right 指针的时候，说明 mid - right 之间的所有的元素都小于 nums[left]
问题： left ++ 或者 right ++ 之前 count ，不然会错哦
问题：不能用 hashMap 存储哦，代笔，因为会有重复值，count 值是所有都小于，而不是右边都小于
md 这道hard 题花了老子三个小时，我是个蠢逼

AC（TODO 抄的题解真的很头疼。。。。）

class Solution {
    private class Pair {
        int val, id;
        Pair(int val, int id) {
            // 记录数组的元素值
            this.val = val;
            // 记录元素在数组中的原始索引
            this.id = id;
        }
    }
    
    // 归并排序所用的辅助数组
    private Pair[] temp;
    // 记录每个元素后面比自己小的元素个数
    private int[] count;
    
    // 主函数
    public List<Integer> countSmaller(int[] nums) {
        int n = nums.length;
        count = new int[n];
        temp = new Pair[n];
        Pair[] arr = new Pair[n];
        // 记录元素原始的索引位置，以便在 count 数组中更新结果
        for (int i = 0; i < n; i++)
            arr[i] = new Pair(nums[i], i);
        
        // 执行归并排序，本题结果被记录在 count 数组中
        sort(arr, 0, n - 1);
        
        List<Integer> res = new LinkedList<>();
        for (int c : count) res.add(c);
        return res;
    }
    
    // 归并排序
    private void sort(Pair[] arr, int lo, int hi) {
        if (lo == hi) return;
        int mid = lo + (hi - lo) / 2;
        sort(arr, lo, mid);
        sort(arr, mid + 1, hi);
        merge(arr, lo, mid, hi);
    }
    
    // 合并两个有序数组
    private void merge(Pair[] arr, int lo, int mid, int hi) {
        for (int i = lo; i <= hi; i++) {
            temp[i] = arr[i];
        }
        
        int i = lo, j = mid + 1;
        for (int p = lo; p <= hi; p++) {
            if (i == mid + 1) {
                arr[p] = temp[j++];
            } else if (j == hi + 1) {
                arr[p] = temp[i++];
                // 更新 count 数组
                count[arr[p].id] += j - mid - 1;
            } else if (temp[i].val > temp[j].val) {
                arr[p] = temp[j++];
            } else {
                arr[p] = temp[i++];
                // 更新 count 数组
                count[arr[p].id] += j - mid - 1;
            }
        }
    }
}

25.翻转对

思路

在merge之前做操作

AC（抄的题解）

public int reversePairs(int[] nums) {
    // 执行归并排序
    sort(nums);
    return count;
}

private int[] temp;

public void sort(int[] nums) {
    temp = new int[nums.length];
    sort(nums, 0, nums.length - 1);
}

// 归并排序
private void sort(int[] nums, int lo, int hi) {
    if (lo == hi) {
        return;
    }
    int mid = lo + (hi - lo) / 2;
    sort(nums, lo, mid);
    sort(nums, mid + 1, hi);
    merge(nums, lo, mid, hi);
}

// 记录「翻转对」的个数
private int count = 0;

private void merge(int[] nums, int lo, int mid, int hi) {
    for (int i = lo; i <= hi; i++) {
        temp[i] = nums[i];
    }
    
    // 进行效率优化，维护左闭右开区间 [mid+1, end) 中的元素乘 2 小于 nums[i]
    // 为什么 end 是开区间？因为这样的话可以保证初始区间 [mid+1, mid+1) 是一个空区间
    int end = mid + 1;
    for (int i = lo; i <= mid; i++) {
        // nums 中的元素可能较大，乘 2 可能溢出，所以转化成 long
        while (end <= hi && (long)nums[i] > (long)nums[end] * 2) {
            end++;
        }
        count += end - (mid + 1);
    }

    // 数组双指针技巧，合并两个有序数组
    int i = lo, j = mid + 1;
    for (int p = lo; p <= hi; p++) {
        if (i == mid + 1) {
            nums[p] = temp[j++];
        } else if (j == hi + 1) {
            nums[p] = temp[i++];
        } else if (temp[i] > temp[j]) {
            nums[p] = temp[j++];
        } else {
            nums[p] = temp[i++];
        }
    }
}

好了 merge sort 全是 hard 我们到此为止先，为了面试而已，没必要硬刚浪费时间对吧！

26. 二叉搜索树中第K小的元素

思路

BST 中序遍历是有序的，第 k 小就是第 k 次递归嘛！

AC

public class PRC_230 {

    int kthValue;

    int count;
    public int kthSmallest(TreeNode root, int k) {
        traverse(root, k);
        return kthValue;
    }

    public void traverse(TreeNode root, int k) {
        if (root == null) {
            return ;
        }

        kthSmallest(root.left,k);
        count ++;
        if (k == count) {
            kthValue = root.val;
        }
        kthSmallest(root.right,k);

    }


}

27.把二叉搜索树转换为累加树

思路

个人比较难理解题目
必须向右先遍历

AC

public class PRC_538 {
    int sum = 0;

    public TreeNode convertBST(TreeNode root) {
        traverse(root);
        return root;
    }

    public void traverse(TreeNode root) {
        if (root == null) {
            return ;
        }
        traverse(root.right);
        sum += root.val;
        root.val = sum;
        traverse(root.left);
    }

    public static void main(String[] args) {
        TreeNode node6 = new TreeNode(6);
        TreeNode node5 = new TreeNode(5);
        TreeNode node7 = new TreeNode(7);
        TreeNode node8 = new TreeNode(8);

        node6.left = node5;
        node6.right = node7;
        node5.left = null;
        node5.right = null;
        node7.right = node8;
        node7.left = null;
        node8.left = null;
        node8.right = null;

        PRC_538 prc = new PRC_538();


    }

}

28. 二叉搜索树中的搜索

思路

简单遍历

AC

		public class PRC_700 {
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null) {
            return  null;
        }

        if(root.val == val){
            return root;
        }else if(root.val > val){
            return searchBST(root.left, val);
        }else{
            return searchBST(root.right, val);
        }

    }
}

29.验证二叉搜索树

思路

左右子树，需要严格遵循 BST 的规则
同时也要保证当前 val ，左边小于 root.val , 右边大于 root.val

AC

public class PRC_98 {
    public boolean isValidBST(TreeNode root) {
        return isValidBST(root, null, null);
    }

    public boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
        if (root == null) {
            return true;
        }

        if(min !=null && root.val <= min.val) return false;
        if(max !=null && root.val >= max.val) return false;

        return isValidBST(root.left, min, root) &&
                isValidBST(root.right, root, max);
    }
}

30.二叉搜索树中的插入操作

思路

就是遍历判断左右 Node 的大小，然后插入

AC

public class PRC_701 {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }
        if(root.val > val){
           root.left = insertIntoBST(root.left, val);
        }else if( root.val < val){
            root.right =insertIntoBST(root.right,val);
        }
        return root;
    }
}

31. 删除二叉搜索树中的节点

思路

跟插入结点相似的遍历，定义好框架
删除是比较复杂的操作，需要分情况讨论
情况一：如果要删除的是叶子结点，那就直接 return null
情况二：如果删除的 Node 只有一个子节点，直接把当前节点换成那个唯一的子节点
情况三：需要删除的 Node 又左右结点，根据 BST 性质，要将当前 Node 替换成左子树最大的，或者右子树最小的。

AC

public class PRC_450 {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root == null){
            return  null;
        }
        if(root.val == key){
            //delete logical
            if(root.left == null) return root.right;
            if(root.right == null) return root.left;
            TreeNode min = getMin(root.right);
            root.right = deleteNode(root.right, min.val);
            min.right = root.right;
            min.left = root.left;
            root = min;

        } else if (root.val > key) {
            root.left = deleteNode(root.left, key);
        }else{
            root.right = deleteNode(root.right, key);
        }
        return root;
    }

    public TreeNode getMin(TreeNode root){
        while (root.left != null) {
            root = root.left;
        }
        return root;
    }

    public static void main(String[] args) {

    }
}

32. 不同的二叉搜索树

思路：

以一个元素作为 root ，那么可以构造的个数为 rightSize * leftSize
所以需要 for 循环遍历 n ，这就是回溯
排除重叠子问题就是备忘录记录，进入方法前判断一下旧的是否，结束方法的时候记录一下，就酱紫。

AC

public class PRC_96 {

    int[][] memo;
    public int numTrees(int n) {
        memo = new int[n + 1][n + 1];
        return count(1, n);
    }
    public int count(int lt, int gt) {
        if(lt > gt) return 1;

        if (memo[lt][gt] != 0) {
            return memo[lt][gt];
        }

        int res = 0;
        for (int i = lt; i <=gt; i++) {

            int leftSize = count(lt, i - 1);
            int rightSize = count(i + 1, gt);
            res += leftSize * rightSize;
        }

        memo[lt][gt] = res;
        return res;
    }
}

(Addition)二叉树的右视图

AC

public class PRC_199 {

    public List<Integer> rightSideView(TreeNode root) {
        if (root == null) {
            return Collections.emptyList();
        }
        List<Integer> res = new LinkedList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode poll = queue.poll();
                if (i == size - 1) {
                    res.add(poll.val);
                }
                if (poll.left != null) {
                    queue.offer(poll.left);
                }
                if (poll.right != null) {
                    queue.offer(poll.right);
                }
            }
        }
        return res;
    }

    public static void main(String[] args) {

        TreeNode treeNode1 = new TreeNode(1);
        TreeNode treeNode2 = new TreeNode(2);
        TreeNode treeNode3 = new TreeNode(3);
        TreeNode treeNode4 = new TreeNode(4);
        TreeNode treeNode5 = new TreeNode(5);
        treeNode1.left = treeNode2;
        treeNode1.right = treeNode3;
        treeNode2.left = null;
        treeNode2.right = treeNode5;
        treeNode3.left = null;
        treeNode3.right = treeNode4;
        treeNode4.left = null;
        treeNode4.right = null;
        treeNode5.left = null;
        treeNode5.right = null;


        PRC_199 prc = new PRC_199();
        System.out.println(prc.rightSideView(treeNode1));
    }
}

33.合并两个有序链表

思路

没啥难度

AC

public class PRC_21 {

    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {


        ListNode dummyHead = new ListNode();
        ListNode head = dummyHead;

        while (list1 != null || list2 != null) {
            if (list1 == null) {
                dummyHead.next = list2;
                list2 = list2.next;
            } else if (list2 == null) {
                dummyHead.next = list1;
                list1 = list1.next;
            }else if (list1.val < list2.val) {
                dummyHead.next = list1;
                list1 = list1.next;
            }else{
                dummyHead.next = list2;
                list2 = list2.next;
            }
                dummyHead  = dummyHead.next;

        }

        return head.next;
    }
}

(优化一下，之前多了一些没有必要判断，被 merge sort 的思路带进去了)

public class PRC_21 {

    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {


        ListNode dummyHead = new ListNode();
        ListNode head = dummyHead;

        while (list1 != null && list2 != null) {
            if (list1.val < list2.val) {
                dummyHead.next = list1;
                list1 = list1.next;
            } else {
                dummyHead.next = list2;
                list2 = list2.next;
            }

            dummyHead = dummyHead.next;
        }

        dummyHead.next = list1 == null ? list2 : list1;

        return head.next;
    }
}

34.分隔链表

思路

就正常的思路，但是有个关键点，head = head.next 不可行，当 lt 和 gt 执行 next 当时候，会把 head 原来的 next 也 next 进去，会形成环路， cpu会飙升的，如果在 prod env 中对吧
所以每次 head.next 的时候需要断开原来的 next，我们只关心 head 的值，而不关心 head.next 后续的情况。

AC

		ublic class PRC_86 {
    public ListNode partition(ListNode head, int x) {

        ListNode lt = new ListNode(-1);
        ListNode ltDummyHead = lt;
        ListNode gt = new ListNode(-1);
        ListNode gtDummyHead = gt;

        while(head!= null) {
            if(head.val <x){
                lt.next = head;
                lt = lt.next;
            }else{
                gt.next = head;
                gt = gt.next;
            }
          // 这里 为什么不写 head = head.next;不断开原来的会成环
            ListNode temp = head.next;
            head.next = null;
            head = temp;
        }
        lt.next = gtDummyHead.next;
        return ltDummyHead.next;
    }
}

动态规划专题

35.反转链表

思路

递归，last Node 只是为了返回一个反转后的头节点，不做其他操作。

AC

public class PRC_206 {

    public ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }

        // 上一层返回回来的结果,也就是最后的结点
        ListNode last = reverseList(head.next);
        //下一层的逻辑

        head.next.next= head;
        head.next = null;

        return last;
    }
}

36.斐波那契数

思路（优化成dp，-> 将 n 优化成 2）

去除重叠子问题

public int fib(int n) {
      int[] memo = new int[n + 1];
      return fib(memo, n);
  }


  public int fib(int[] memo, int n) {
      if(n == 1 || n ==0){
          return n;
      }
      if(memo[n]!=0){
          return memo[n];
      }
      memo[n] = fib(memo, n - 1) + fib(memo, n - 2);

      return memo[n];

  }

37.零钱兑换

思路

简单说下，这个自顶向下的递归，从题目的 11 块钱要几个硬币，我就需要6 块钱，9块钱和 10 块钱需要多少…. ，然后就是用 6， 9 ， 10 继续向下面去推断，直到最后的 base case ，0 块钱就是正好需要 0个，然后返回上一个问题，我们知道下一次正好是 0 块的时候，需要 0个硬币，加上我们这一次我就需要一个硬币啦，所以就是 0 + 1 个硬币，可以凑出我们当前的价格。
就这样一层层往上面去推断。

AC

int[] memo;

public int coinChange(int[] coins, int amount) {
    int[] memo = new int[amount + 1];
    Arrays.fill(memo, -100);
    return dp(coins, amount);

}

public int dp(int[] coins, int amount) {
    if(amount == 0) return 0;
    if(amount < 0) return  -1;
    if (memo[amount] != -100) {
        return memo[amount];
    }

    int res = Integer.MAX_VALUE;
    for (int coin : coins) {

        int subProblem = dp(coins, amount - coin);

        if(subProblem == -1) continue;

        res = Math.min(res, subProblem + 1);

    }
    memo[amount] = res == Integer.MAX_VALUE ? -1 : res;
    return memo[amount];


}

38. 最长递增子序列

思路

dp[i] 表示 nums[i]的最长子序列
我们就要知道比 i 小的最长的子序列是多少
所以 fori 里面还要多加一个 0，i 的循环去找比 i 的 dp[j] 找出最大的，最后加上当前的情况就是 +1

AC

public class PRC_300 {

//    输入：nums = [10,9,2,5,3,7,101,18]
//    输出：4
//    解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

    public int lengthOfLIS(int[] nums) {
        // dp[i] 表示 nums[i] 的最长子序列
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        for (int i = 0; i < nums.length; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[j] < nums[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
        }
        int res = 0;
        for (int i = 0; i < nums.length; i++) {
            res = Math.max(dp[i], res);
        }

        return res;
    }

    public static void main(String[] args) {
        PRC_300 prc = new PRC_300();
        System.out.println(prc.lengthOfLIS(new int[]{10, 9, 2, 5, 3, 7, 101, 18}));

    }
}

39. 俄罗斯套娃信封问题

思路

选择一个可以装入的信封，我们就必须要确认长度或者宽度的顺序，比如我们确定的宽度，然后我们就要循环去找长度的最长递增子序列，这样就解决了

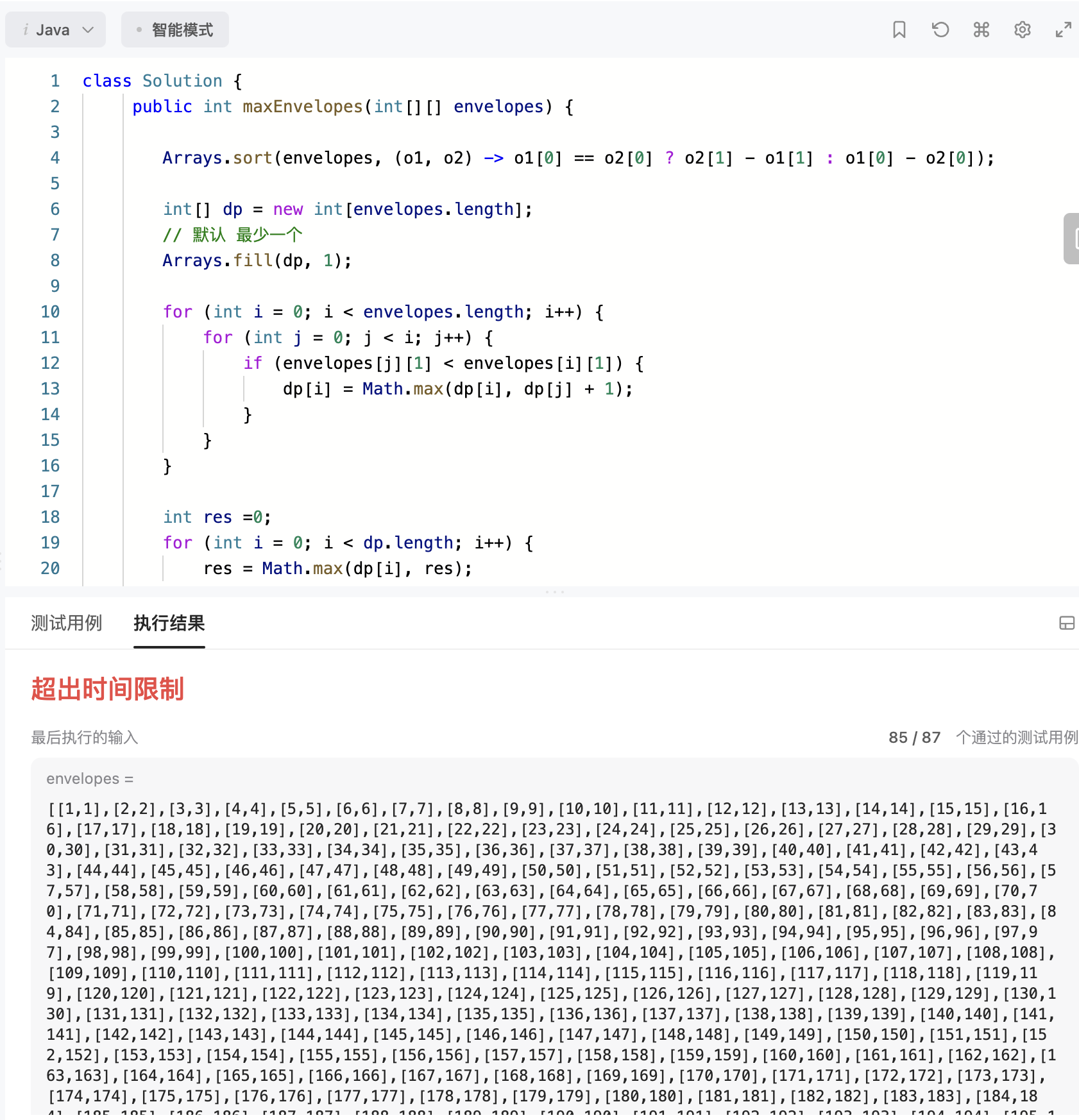
AC

用java真的没有办法，很慢，想不到优化方案了

java真的没有办法

class Solution {
    public int maxEnvelopes(int[][] envelopes) {

        Arrays.sort(envelopes, (o1, o2) -> o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0]);

        int[] dp = new int[envelopes.length];
        // 默认 最少一个
        Arrays.fill(dp, 1);

        for (int i = 0; i < envelopes.length; i++) {
            for (int j = 0; j < i; j++) {
                if (envelopes[j][1] < envelopes[i][1]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
        }

        return  Arrays.stream(dp).max().getAsInt();

    }
}

1. Two Sum(两数之和)

思路

2. Add Two Numbers (两数相加)

思路

code

3. Longest Substring Without Repeating Characters (无重复字符的最长子串)

思路

AC ( 待优化)

4. Median of Two Sorted Arrays (寻找两个正序数组的中位数)

思路

AC

5. Longest Palindromic Substring (最长回文子串)

思路

AC(动态规划，求最长公共字串，最后找回文)

AC 中心扩展

6. 3Sum (三数之和)

AC(自己两年的代码，现在的我竟然看不懂，而且写不出来)

7. Maximum Subarray (最大子序和)

思路

AC

8. Reverse Integer (整数反转)

思路

AC（不动脑子做法）

9.Container With Most Water (盛最多水的容器)

思路

AC

10.Trapping Rain Water (接雨水)

思路

AC

11. Valid Parentheses (有效的括号)

思路

AC

树专题

12. 二叉树的最大深度

思路

AC（M1）

AC(M2)

13. 二叉树的前序遍历

思路

AC(M1)

AC(M2)

AC(M3)

14. 二叉树的直径

思路

AC

15.翻转二叉树

思路

AC（M1）

AC(M2)

16.填充每个节点的下一个右侧节点指针

思路

AC

17. 二叉树展开为链表

思路

AC

18.最大二叉树

思路

AC

19.从前序与中序遍历序列构造二叉树

思路

AC

20. 从中序与后序遍历序列构造二叉树

思路

AC（ 一遍过，思路及其正确）

21. 二叉树的序列化与反序列化

思路：

AC

22.寻找重复的子树

思路：

AC

23.归并排序（早就会了）

24.计算右侧小于当前元素的个数（hard）

思路:

AC（TODO 抄的题解真的很头疼。。。。）

25.翻转对

思路

AC（抄的题解）

好了 merge sort 全是 hard 我们到此为止先，为了面试而已，没必要硬刚浪费时间对吧！

26. 二叉搜索树中第K小的元素

思路

AC（一遍过，思路及其正确）