PAT 1010 Radix

题目

思路

• 将两个进行比较多数都转变成10进制

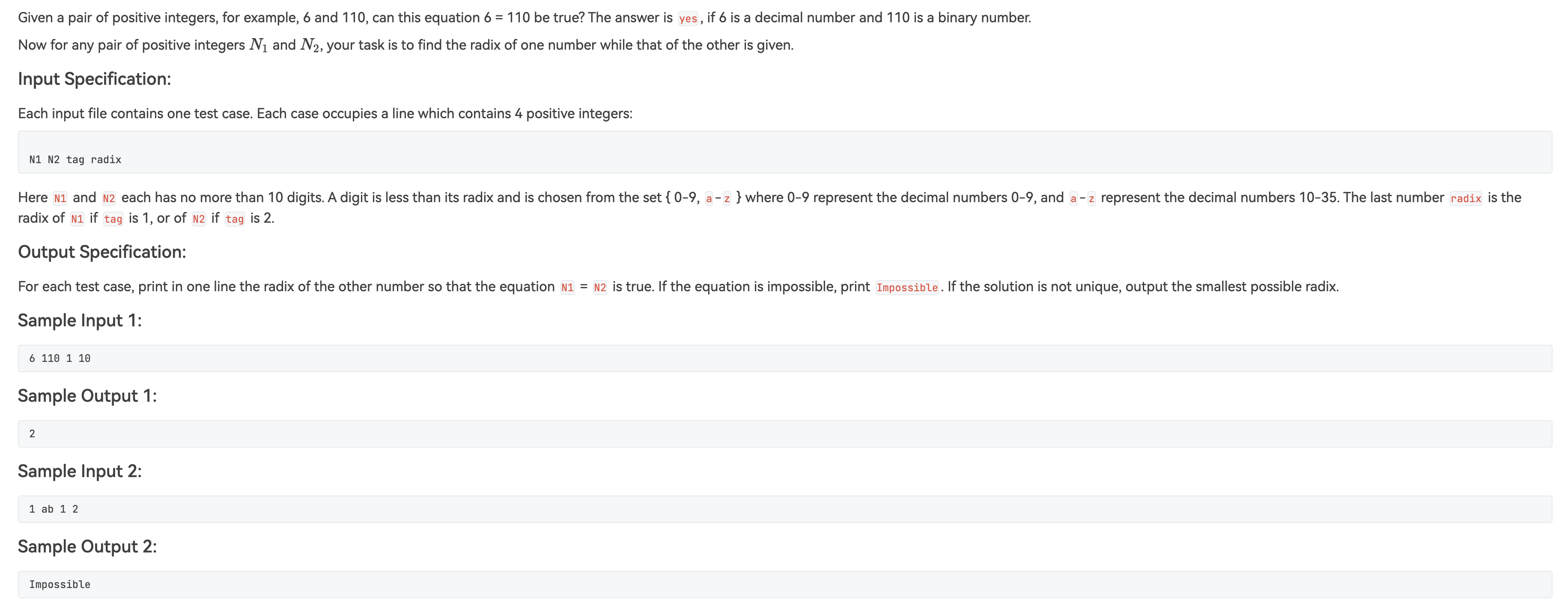
​ long long itoa(string n , long long radix)

​ 这边都是需要 long long 类型多， 因为 radix 和 进制转化都会溢出

另一种容易理解的实现

• 假设 此时 tag =1 ，那么需要比较的就是N2， 要从 radix[left, right] 中一个个 遍历， 是的 N2转化的 radix 进制的结果 和 N1 转化成 radix2 （参数给的 radix）进制一样；

     1.     确定 left ， 最小值 一定是 给定 N2 中的 最大的 digit + 1。
     1.     确定 right ，我们不知道 ，但一定 比 N1 进制转化后的小，设为 itoa(N2, radix) ,但有可能 left 比 itoa(N2, radix) 大 ， 所以 right = max(left , itoa(N2, radix);
  

• 二分查找

​ 我们要注意 ，当 发生进制转化的时候， 很有肯能发生溢出， 毕竟10位数的运算真的很大， 所以当 发生溢出的时候，不单单是 判断 a > b , 还要判断 a < 0 ? 是否成立。（a < 0 表示结果 特别大，但是溢出了，缺失精度，用负数表示）

long long equationResult(string dest , string src, long long radix)

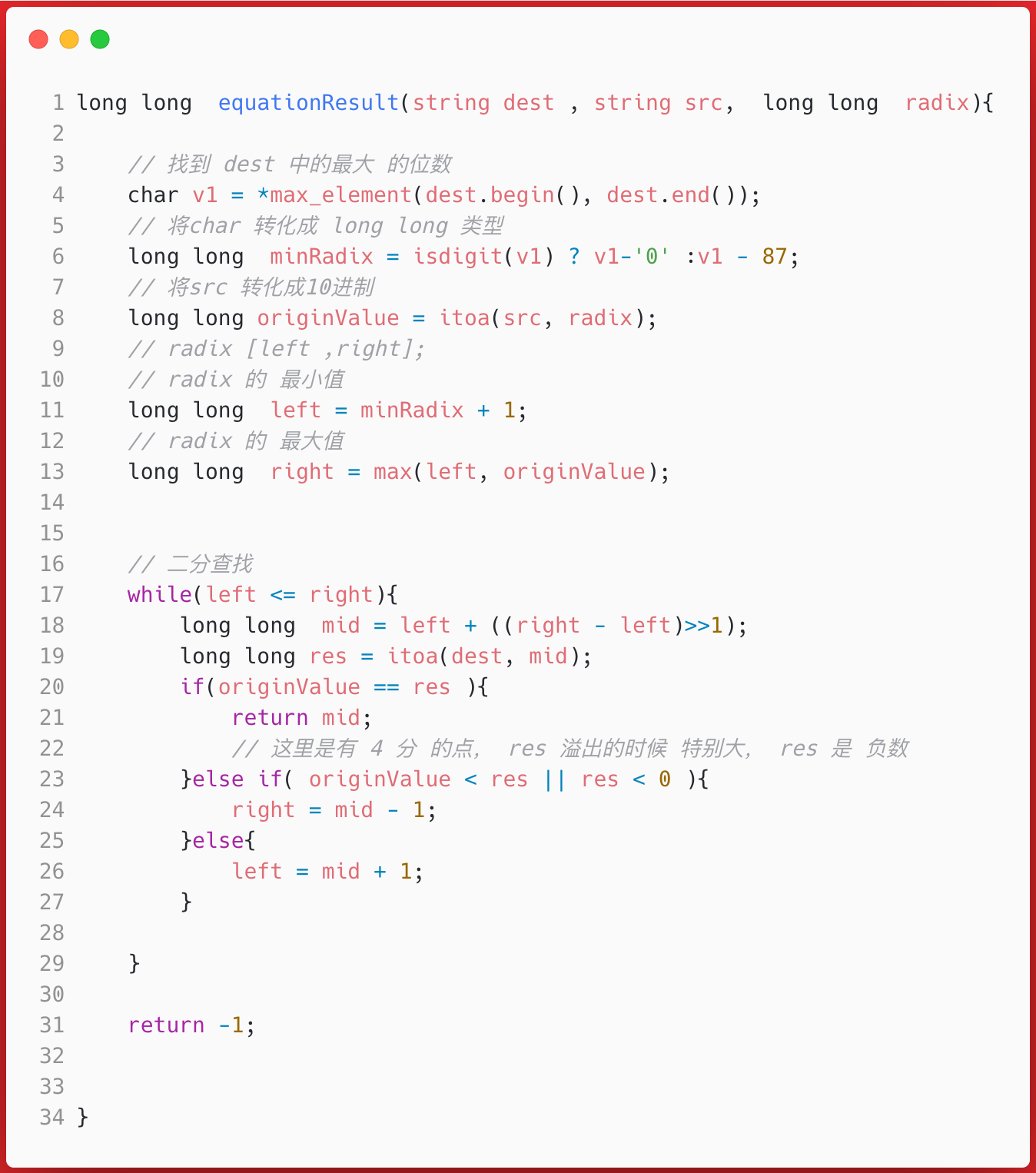
Main()

Conclusion

难点：

1. 怎么写一个 进制转化的函数，
2. 判断溢出
3. 考虑 范围 不仅 res 要用 long long, radix 也要用 long long , long long = __int64

二分不难，细节很难。